Angolo interno minimo di un poligono↵

Come trovare l'angolo interno più piccolo (più stretto) di un poligono utilizzando il calcolatore di campi.

Problema↵

Dato un poligono, si vuole calcolare quale sia l'angolo interno più piccolo formato dai suoi vertici. Questo può essere utile per:

Identificare poligoni con angoli molto stretti
Validare geometrie
Analizzare la forma degli edifici
Controllo qualità dei dati geometrici

Soluzione con espressione↵

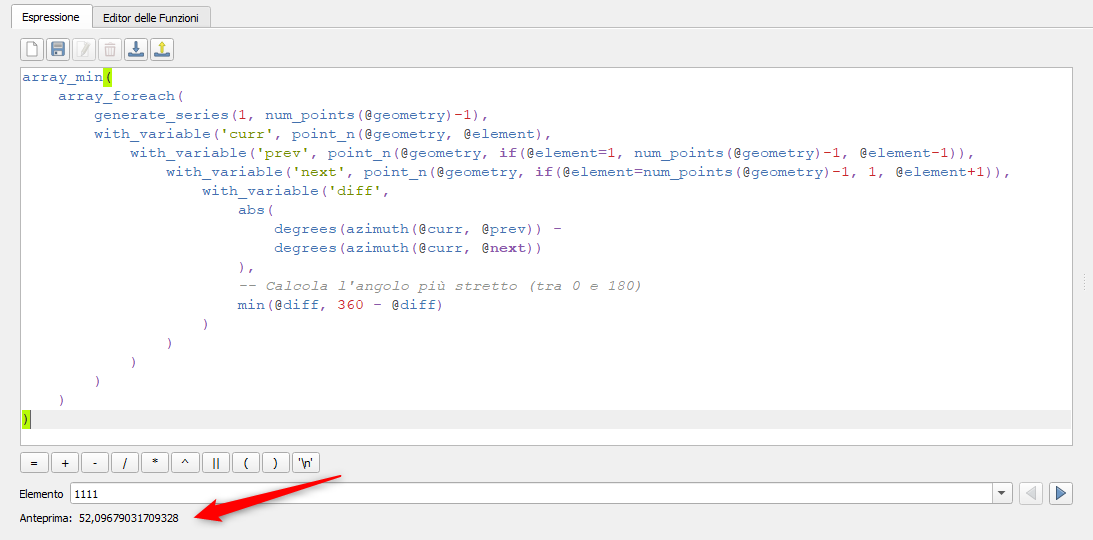
Espressione completa↵

array_min(
    array_foreach(
        generate_series(1, num_points(@geometry)-1),
        with_variable('curr', point_n(@geometry, @element),
            with_variable('prev', point_n(@geometry, if(@element=1, num_points(@geometry)-1, @element-1)),
                with_variable('next', point_n(@geometry, if(@element=num_points(@geometry)-1, 1, @element+1)),
                    with_variable('diff', 
                        abs(
                            degrees(azimuth(@curr, @prev)) - 
                            degrees(azimuth(@curr, @next))
                        ),
                        -- Calcola l'angolo più stretto (tra 0 e 180)
                        min(@diff, 360 - @diff)
                    )
                )
            )
        )
    )
)

Output: Il valore dell'angolo interno minimo espresso in gradi (0-180°)

Spiegazione dettagliata↵

1. Generazione della sequenza di vertici↵

generate_series(1, num_points($geometry)-1)

Cosa fa:

num_points($geometry) → Conta il numero totale di vertici del poligono
generate_series(1, n-1) → Crea una sequenza da 1 a n-1 (esclude l'ultimo vertice perché nei poligoni il primo e l'ultimo coincidono)

Esempio pratico:

Per un poligono con 6 vertici, genera: [1, 2, 3, 4, 5]

2. Iterazione sui vertici con array_foreach↵

array_foreach(
    generate_series(...),
    ...
)

Cosa fa:

Itera su ogni numero della sequenza
Per ogni iterazione, @element contiene il numero del vertice corrente
Esegue il calcolo dell'angolo per ciascun vertice

3. Identificazione dei tre punti consecutivi↵

with_variable('curr', point_n($geometry, @element),
  with_variable('prev', point_n($geometry, if(@element=1, num_points($geometry)-1, @element-1)),
    with_variable('next', point_n($geometry, if(@element=num_points($geometry)-1, 1, @element+1)),
      ...
    )
  )
)

Cosa fa:

@curr → Vertice corrente (quello per cui calcoliamo l'angolo)
@prev → Vertice precedente (gestisce il caso del primo vertice)
@next → Vertice successivo (gestisce il caso dell'ultimo vertice)

Gestione casi speciali:

Se @element = 1 (primo vertice): @prev diventa l'ultimo vertice reale
Se @element = num_points-1 (ultimo vertice): @next diventa il primo vertice

4. Calcolo dell'angolo↵

with_variable('diff', 
  abs(
    degrees(azimuth(@curr, @prev)) - 
    degrees(azimuth(@curr, @next))
  ),
  min(@diff, 360 - @diff)
)

Cosa fa (passo per passo):

azimuth(@curr, @prev) → Calcola l'azimut (direzione) dal vertice corrente a quello precedente (in radianti)
azimuth(@curr, @next) → Calcola l'azimut dal vertice corrente a quello successivo
degrees(...) → Converte da radianti a gradi
Sottrazione → Calcola la differenza tra i due angoli
abs(...) → Prende il valore assoluto (angolo sempre positivo)
min(@diff, 360 - @diff) → Normalizza l'angolo tra 0° e 180° (sceglie l'angolo più piccolo tra i due possibili)

Esempio numerico:

Se l'azimut verso @prev è 45° e verso @next è 135°: - Differenza: |45° - 135°| = 90° - min(90°, 360° - 90°) = min(90°, 270°) = 90°

Se la differenza fosse 270°: - min(270°, 360° - 270°) = min(270°, 90°) = 90°

5. Selezione del minimo↵

array_min(
  array_foreach(...)
)

Cosa fa:

array_foreach crea un array con tutti gli angoli calcolati per ogni vertice
array_min seleziona il valore minimo dall'array

Esempio:

Se gli angoli sono [120°, 95°, 75°, 110°, 85°], restituisce 75°

Come utilizzare l'espressione↵

Passaggi:↵

Aprire la tabella degli attributi del layer poligonale
Aprire il Calcolatore di Campi (icona dell'abaco o Ctrl+I)
Configurare il nuovo campo:
Crea un nuovo campo
Nome campo: angolo_min (o il nome che si preferisce)
Tipo di campo: Numero decimale (double o real)
Lunghezza: 10
Precisione: 2
Incollare l'espressione nell'editor
Cliccare OK per calcolare il campo

Applicazioni pratiche↵

1. Selezione poligoni con angoli stretti↵

Selezionare tutti i poligoni con angoli interni minori di 30°:

"angolo_min" < 30

2. Validazione geometrie↵

Identificare edifici con angoli troppo acuti (possibili errori di digitalizzazione):

"angolo_min" < 15

3. Tematizzazione↵

Colorare i poligoni in base all'angolo minimo:

Rosso: angoli < 30° (geometrie problematiche)
Giallo: angoli tra 30° e 60°
Verde: angoli > 60° (geometrie regolari)

Varianti dell'espressione↵

Trovare l'angolo massimo invece del minimo↵

Sostituire array_min con array_max:

array_max(
  array_foreach(...)
)

Calcolare la media degli angoli interni↵

Sostituire array_min con array_mean:

array_mean(
  array_foreach(...)
)

Contare quanti angoli sono sotto una soglia↵

array_length(
  array_filter(
    array_foreach(...),
    @element < 30
  )
)

Note importanti↵

Tipo di geometria↵

L'espressione funziona con:

✅ Poligoni singoli (Polygon)
⚠️ Multi-poligoni (solo il primo anello del primo poligono)
❌ Linee e punti (non applicabile)

Anelli interni (buchi)↵

L'espressione calcola solo l'anello esterno del poligono. Per analizzare anche i buchi interni, serve un'espressione più complessa.

Performance↵

L'espressione è relativamente complessa. Su dataset molto grandi (migliaia di poligoni con molti vertici):

Considerare di salvare il risultato in un campo fisico
Valutare l'uso di Processing Python per performance migliori

Unità di misura↵

Il risultato è sempre in gradi (0-180°), indipendentemente dal sistema di coordinate del layer.

Risoluzione problemi↵

Risultato NULL↵

Causa: Il poligono ha meno di 3 vertici (geometria invalida)

Soluzione: Verificare e correggere le geometrie con "Controlla validità"

Risultato 0↵

Causa:

Tre vertici consecutivi sono perfettamente allineati, formando un angolo di 180° (angolo piatto). Questo significa che:

Il vertice intermedio giace esattamente sulla linea tra i due vertici adiacenti
Non c'è realmente un "angolo" in quel punto
La geometria potrebbe avere un vertice ridondante

Esempi tipici:

Poligoni con vertici non necessari lungo un lato retto
Errori di digitalizzazione
Geometrie semplificate male

Soluzione:

Rimuovere vertici ridondanti: Strumenti → Geometria → Semplifica geometria
Verificare manualmente: Usare lo strumento di modifica vertici per controllare
Se intenzionale: Il valore 0° è corretto per quella geometria

Risultato 180↵

Causa:

Angolo molto ampio (quasi piatto ma dall'altra parte)

Soluzione:

Verificare la geometria, potrebbe essere corretta o indicare un errore di digitalizzazione

Errore "point_n not found"↵

Causa: Versione di QGIS troppo vecchia

Soluzione: Aggiornare QGIS alla versione 3.0 o superiore

Soluzioni alternative↵

Virtual Layer (SQL con Spatialite)↵

Non esiste una funzione SQL standard equivalente. È necessario usare l'espressione QGIS o uno script Python.

Processing Python↵

Per analisi più complesse o dataset molto grandi, considerare uno script Python che usa la libreria Shapely:

from shapely.geometry import Point
import math

def calculate_min_angle(geom):
    coords = list(geom.exterior.coords)[:-1]  # Escludi ultimo punto
    angles = []

    for i in range(len(coords)):
        prev = coords[i-1]
        curr = coords[i]
        next_pt = coords[(i+1) % len(coords)]

        # Calcola angoli
        angle1 = math.atan2(prev[1]-curr[1], prev[0]-curr[0])
        angle2 = math.atan2(next_pt[1]-curr[1], next_pt[0]-curr[0])

        diff = abs(math.degrees(angle1 - angle2))
        angle = min(diff, 360 - diff)
        angles.append(angle)

    return min(angles)

Funzioni e variabili utilizzate: